Air Source Heat Pump
Contents
Basic principle of the Air Source Heat Pump (ASHP)
A Heat Pump is a mechanical device for extracting heat from a lower-temperature source and delivering it to a higher-temperature medium. The word 'pump' is used by analogy with that familiar device for raising water from a lower to higher elevation. In either case, mechanical energy is expended to reverse a natural, spontaneous flow of heat from hot to cold - or water from above to below. The operating principal for a heat pump is very similar to a refrigerator or an air conditioning unit; the main distinction being whether heating or cooling is regarded as the 'useful' task; the term heat pump is generally used where heating is the desired result. From the energy balance:
Heatextracted + Workinput = Heatoutput
it can be seen that output heat is always greater than the input work and the ratio of heat to work necessarily exceeds 1. This is sometimes referred to (inaccurately) as heat pumps having an efficiency greater than 100%; engineers prefer the term 'coefficient of performance' or COP:
COP = Heatoutput / Workinput
Under favourable conditions, an electric-powered ASHP with a HFC working-fluid operating to a reverse Rankine cycle may achieve COP values in the range 2.5 to 3; that is for every 1 kW-h of electricity consumed, 2.5-3 kW-h of heat is produced. The COP is not, however a fixed value. By extending the pump analogy the greater the head of water pumped, the more power is required. Likewise heat pumps perform less efficiently on cold days than mild ones - the opposite way to what might be desired
A typical domestic ASHP, positioned outside the house, is a box-shaped housing containing fans plus the mechanisms to extract heat. Fans draw outdoor air over rows of tubes containing the cold working fluid which, being even colder than the outside air is 'warmed' by the air (relatively speaking); the air is simultaneously cooled. Through a somewhat complex closed-loop cycle the working fluid so warmed is first compressed, raising its temperature so it can provide 'useful' heat. It is then expanded, returning to its original cold state and ready to absorb more heat from the air.
Heat pumps of the air-to-air type extract heat from outdoor air to heat indoor air which is circulated for space heating only (like a convection heater). Air-to-water extract heat in exactly the same way but provide heat to the house in the form of hot water, which can be used for both space heating via the central heating system and domestic hot water, potentially replacing the gas boiler and the immersion heater
Heat availability and performance in the UK climate
In calm air conditions, the heat in a volume of air surrounding one individual property can be calculated from its dimensions, the density and specific heat capacity of air and the air's temperature before and after heat is extracted. So for a plot size of 12 metres by 18 to a height of 10 metres (2,160 m³), an initial temperature of 10°C and final temperature 1°C
Density of air @ 1 atmosphere / 10°C = 1.25 kg/m³ Specific heat capacity of air @ 1 atmosphere / 10°C = 1.00 kJ/kg/°C Mass of air = 1.25 * 2160 = 2,700 kg Heat content = 2,700 * 1.00 * (10 - 1) = 24,300 kJ (or 6.8 kW-h)
An ASHP operating at a COP of 3 would produce ~ 10.2 kW-h for the house (6.8 kW-h air-sourced heat plus 3.4 kW-h electricity = 10.2 kW-h; 10.2 / 3.4 = 3, the COP) which means the house could be heated at 2kW for 5 hours
10°C is the year-round average temperature (day & night, all seasons) for much of the UK and would be regarded as mild - in winter. ASHPs have been used successfully in Scandinavian climates with air temperatures -10°C or lower - but this is dry air. With the exception of this Paper by Professor David Strong FLUKE has seen little research on the practical application of ASHPs, under conditions which anyone with a passing familiarity with the British 'maritime' climate would recognise
- cold - say 1 to 5°C
- wet - rain, drizzle, mist etc.
under these conditions it is a near-certainty the ASHP will ice-up causing it not only to cease providing heat completely but actually require a heat input for the defrost cycle
Some real-life consumers' experiences are documented here
If a large array of ASHPs are adopted as in the illustration resulting in the surrounding air temperature dropping from 10°C to 1°C, according to the 'degree-days' method of estimating heat demand, the rate of heat loss from a house might be expected to increase by a factor of (15.5-1)/(15.5-10) = 2.6 times
A layer of cold air close to the ground - when it occurs naturally - is called a temperature inversion, often associated with a low level layer of mist or fog. The phenomenon is also associated with trapping air pollutants.
The marketing view
The consumers' view
Some real-life consumers' experiences are documented at Carbon Commentary
A simple model for estimating Air Source Heat Pump performance
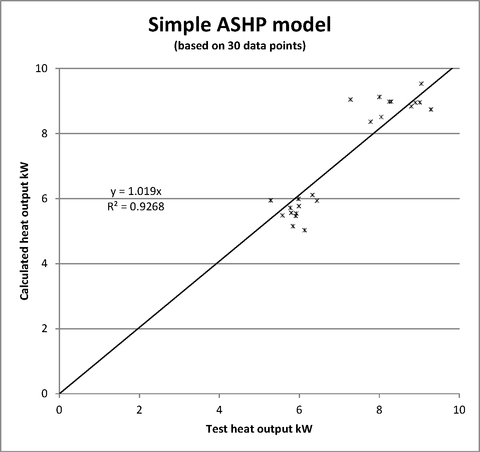
The Building Research Establishment carried out tests BRE Test Report on a Mitsubishi PUHZ-W90VHA air-to-water heat pump and the test results presented in table 3 of that document were analysed against a reverse-Carnot cycle (original work by FLUKE). The Carnot cycle describes the maximum theoretical efficiency of ANY thermodynamic process and has the advantage that it can be calculated without any knowledge of the device, but simply from two temperatures expressed in degrees Kelvin: the cold and hot limits of the process, in this case the outside air heat source temperature and the supply temperature to hot water for space heating. So the two equations are
COPACTUAL = Heat output (kW) / Electrical power input (kW) … as reported
COPCARNOT = 1 / ( 1 - TCOLD / THOT ) … T in Kelvin
which when expressed in Celsius and rearranged gives:
COPCARNOT = (tHOT + 273) / (tHOT - tCOLD) … t in Celsius
The average value over 30 tests for COPACTUAL/COPCARNOT is 0.342 so the COP value for the Mitsubishi heat pump can be estimated simply from the outdoor air temperature and the hot water supply temperature from the equation:
COPCALC = 0.342 * (tHOT + 273) / (tHOT - tCOLD) … t in Celsius
Other makes and models of ASHP may be expected to have factors slightly higher or lower than 0.342. To assess the validity of the model, calculated versus actual (test) values of COP are presented below:
Application of the model to a case study
Armed with a simple equation to calculate COP and 'degree day' data averaged over 20 years (method discussed elsewhere) , a case study 'typical' house can be modelled based on providing heat for space heating and domestic hot water using the heat pump instead of a gas boiler that would otherwise have a 'medium' gas consumption of 12,000 kW-h per year (OFGEM). The supply temperature is 55°C so that the ASHP can be used as a retrofit to a normal central heating system for economy (compared to say, replacing with brand new low-temperature underfloor heating). The outside temperature is assumed to be constant at the monthly average and heat demand is weighted accordingly
| Month | 20-year average degree days |
Days/month | Mean temperature below 15.5C |
Mean temperature | THOT K | TCOLD K | COPCARNOT | COPCALC | Mean monthly heat demand kW |
Mean monthly motor power kW |
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D=B/C | E=15.5-D | F | G=E+273 | H | I=0.342*H | J | K=J/I |
| January | 362 | 31 | 11.7 | 3.8 | 328 | 276.8 | 6.41 | 2.19 | 2.43 | 1.11 |
| February | 318 | 28 | 11.4 | 4.1 | 328 | 277.1 | 6.45 | 2.21 | 2.13 | 0.97 |
| March | 299 | 31 | 9.6 | 5.9 | 328 | 278.9 | 6.67 | 2.28 | 2.00 | 0.88 |
| April | 235 | 30 | 7.8 | 7.7 | 328 | 280.7 | 6.93 | 2.37 | 1.57 | 0.66 |
| May | 156 | 31 | 5.0 | 10.5 | 328 | 283.5 | 7.37 | 2.52 | 1.05 | 0.42 |
| June | 90 | 30 | 3.0 | 12.5 | 328 | 285.5 | 7.72 | 2.64 | 0.60 | 0.23 |
| July | 45 | 31 | 1.5 | 14.0 | 328 | 287.0 | 8.01 | 2.74 | 0.30 | 0.11 |
| August | 52 | 31 | 1.7 | 13.8 | 328 | 286.8 | 7.97 | 2.72 | 0.35 | 0.13 |
| September | 95 | 30 | 3.2 | 12.3 | 328 | 285.3 | 7.69 | 2.63 | 0.64 | 0.24 |
| October | 183 | 31 | 5.9 | 9.6 | 328 | 282.6 | 7.22 | 2.47 | 1.23 | 0.50 |
| November | 270 | 30 | 9.0 | 6.5 | 328 | 279.5 | 6.76 | 2.31 | 1.81 | 0.78 |
| December | 348 | 31 | 11.2 | 4.3 | 328 | 277.3 | 6.47 | 2.21 | 2.33 | 1.05 |
| Totals | 2453 | 11,967 | 5,147 | |||||||
| °day | kW-hth/year | kW-he/year |
Economics
According to the Money Advice Service the average cost to the UK consumer in 2018 of gas was 4.5p per kW-h and of electricity 18.4p per kW-h. 12,000 kW-h of heat would therefore cost £540 from a conventional gas boiler compared to £947 from an ASHP. However, under the Renewable Heat Incentive (RHI) - a government subsidy scheme designed to encourage uptake of renewable technologies - applicants can claim 10.71p per kW-h for heat provided by an ASHP, so an income of £1,285 per year, for 7 years.
The Domestic RHI scheme scheme closes to new applications at the end of 31 March 2022.
Indicative cost for a complete ASHP system is £5,000-£10,000 see Centre for Sustainable Energy Appendix C. Taking the mid-value (£7,500) costs over a 20 year period can be compared:
- Status quo (gas boiler); cost of gas = £10,800
- ASHP (equipment cost + electricity - RHI payments) = £17,445 (post 31 March 2022 £26,440)
Conclusions
Air Source Heat Pump (ASHP) technology is a method for converting one unit of electrical energy to two - or more - units of heat energy.
Considering ASHP adoption is a central plank of the UK government's strategy for decarbonising home heating, ASHP application in Britain's cold, wet maritime climate has NOT been well studied
In original work by FLUKE performance test results (by BRE) for an ASHP were modelled with reasonable accuracy (R2 = 0.9268). The derived equation depends only on outside temperature, heat supply temperature and one empirically determined constant.
Using the equation, for the case study conditions described above the ASHP could deliver 12,000 kW-h of heat per year, as space heating and domestic hot water to the house for the expenditure of 5,150 kW-h electrical power. This would represent a COP value of 2.33 - rather less the figure 2.5 to 3 sometimes claimed for the technology
Even allowing for the RHI subsidy payments, ASHP is more expensive than a gas boiler. If the ASHP were supplied free-of-charge and RHI payments were received, the cost for ASHP is marginally less