Types of Equilibrium
Contents
Stable, unstable and neutral equilibria
A cone sitting on its base is in a state of stable equilibrium. The downward force of the cone's weight, acting through the centre of gravity is balanced by the reaction force of the ground. The reaction force is equal in size, opposite in direction and perfectly aligned to the weight force. If the cone is pushed aside, the cone's weight still acts through its centre of gravity, but the reaction force is no longer aligned. The reaction now acts at the point of contact between the cone's edge and the ground. The two opposing and misaligned forces create a couple which produces torque tending to twist the cone towards the original, equilibrium position - and can be perceived as the cone "pushing back". Irrespective of which direction the cone is pushed, the reaction force acts to return the cone to the original, equilibrium state, which is why it is termed "stable"
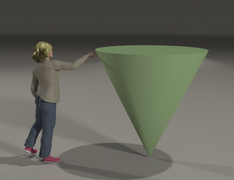
A cone balanced on its point is in a state of unstable equilibrium. As before, the downward force of the cone's weight, acting through the centre of gravity is balanced by the reaction force of the ground. If the cone is pushed aside - even infinitesimally - the couple created by the two opposing and misaligned weight and reaction forces produce torque twisting the cone even further from the initial position and the cone will swiftly topple. An unstable equilibrium is more than anything a theoretical curiosity - at best it could only exist as a transient state
Neutral equilibrium is a special case where no state is more favourable than another e.g. where the cone is lying on it side
Static and Dynamic Equilibria
The former three examples - stable, unstable and neutral - are all static equilibria. In chemistry, in biology and in some physical systems a state of dynamic equilibrium can exist. So consider a reversible chemical reaction where two reagents, A and B react to form a product C:
A + B ⇄ C
At first, only A and B are present. Later some C is formed, the reaction is proceeding. Given sufficient time the reaction will reach equilibrium - with A, B and C all reaching a constant, equilibrium concentration. At a macroscopic level, the reaction has - apparently - stopped, nothing is "happening". At the molecular level, however, A + B are continuing to form C - and C is continuing to decompose into A and B at exactly the same rate. This is dynamic equilibrium.
The equivalence of forward and reverse reaction rates is necessarily so - if it were not - say the forward reaction were greater, then A + B would be consumed faster than they were produced, until their concentration was reduced to the extent where the rates did balance. Chemists can exploit this phenomenon; for example to increase the conversion of A to C, by adding B this "drives" the reaction from the left to right.
In biology, the term homeostasis is used for the highly complex dynamic equilibrium systems such as the regulation of body temperature in warm blooded animals.
Le Chatelier's principle
Le Chatelier's principle is usually expressed as a law of chemistry, though there is no reason why it shouldn't be applied to equilibrium systems in general. It asserts that when ANY factor that impacts a dynamic equilibrium: concentration, temperature, pressure … is manipulated, the system will change in response to that factor until a new equilibrium is reached and furthermore that change tends to oppose and counteract the manipulated factor. Suppose the reversible reaction described above were exothermic (heat producing) i.e.
A + B ⇄ C + heat
then the effect of raising temperature is to force the reaction backwards (more A + B, less C) so absorbing heat and mitigating - though incompletely - the rising temperature.
There is a parallel between a stable static equilibrium and the behaviour of a dynamic equilibrium described by Le Chatelier's principle. In both cases, if you push a system away from equilibrium, it pushes back in the direction that would restore the status quo.
Gaia hypothesis
James Lovelock postulated that the entire planet constitutes an intricate physical/chemical/biological system: "Gaia" (Mother Earth - though never intended to suggest a literal climate-regulating deity or world-spirit). Gaia actively regulates planetary conditions to sustain a benign environment for the biosphere. Lovelock gave his theory more weight by producing an early computer model called DaisyWorld demonstrating how populations of black (heat absorbing) and white (reflective) daisies would prosper or decline all according to a credible biological simulation, thus maintaining a viable temperature for all.
It is a stretch to describe the whole planet in terms either of stable equilibria or Le Chatelier's principle. Yet the premise that the our climate was precariously balanced right up to the industrial revolution and is about to be toppled by us begs the question: "why didn't it fall before now?"
Equilibria (and surely Gaia is the mother of them all) have a propensity to normalise. This is no grounds for complacency about the climate - but it may offer a little hope to counter the despairing talk of tipping-points and cliff-edges